More Iso 2768 Hole Tolerance H7 images.
Tolerances and fits This book includes tables and calculations for easy option of fits of machine parts and determination of their dimensional tolerances and deviations. Using this tool the following tasks can be solved:. Selection of suitable fits of machine parts according to the international standard ISO 286. Determination of dimensional tolerances and deviations of machine parts according to the international standard ISO 286. Selection of preferred fits of machine parts and determination of their dimensional tolerances and deviations according to ANSI B4.1. Determination of non-prescribed limit deviations of linear and angular dimensions according to ISO 2768. Automatic design of a fit for the given clearance or fit interference respectively.
The data, procedures, algorithms and specialized literature and standards ANSI, ISO, DIN and others were used in the calculations. List of standards: ANSI B4.1, ANSI B4.2, ISO 286, ISO 1829, ISO 2768, EN 20286, JIS B 0401.
Information on the syntax and control of the calculation can be found in the document '. It is necessary that the dimensions, shape and mutual position of surfaces of individual parts of mechanical engineering products are kept within a certain accuracy to achieve their correct and reliable functioning. Routine production processes do not allow maintenance (or measurement) of the given geometrical properties with absolute accuracy. Actual surfaces of the produced parts therefore differ from ideal surfaces prescribed in drawings. Deviations of actual surfaces are divided into four groups to enable assessment, prescription and checking of the permitted inaccuracy during production:. Dimensional deviations.
Shape deviations. Position deviations.
Surface roughness deviations This toll includes the first group and can therefore be used to determine dimensional tolerances and deviations of machine parts. As mentioned above, it is principally impossible to produce machine parts with absolute dimensional accuracy. In fact, it is not necessary or useful. It is quite sufficient that the actual dimension of the part is found between two limit dimensions and a permissible deviation is kept with production to ensure correct functioning of engineering products. The required level of accuracy of production of the given part is then given by the dimensional tolerance which is prescribed in the drawing. The production accuracy is prescribed with regards to the functionality of the product and to the economy of production as well.
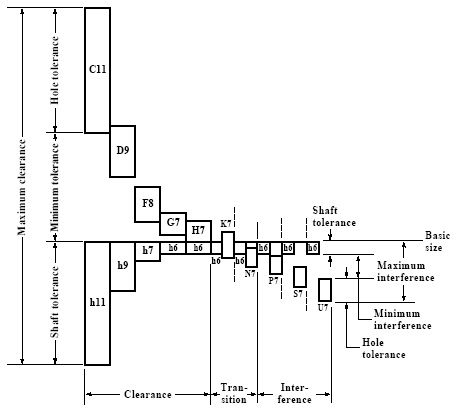
A coupling of two parts creates a fit whose functional character is determined by differences of their dimensions before their coupling. Basic size Dmax, Dmin. Limits of size for the hole dmax, dmin. Limits of size for the shaft ES.
Hole upper deviation EI. Hole lower deviation es. Shaft upper deviation ei. Shaft lower deviation Depending on the mutual position of tolerance zones of the coupled parts, 3 types of fit can be distinguished:.
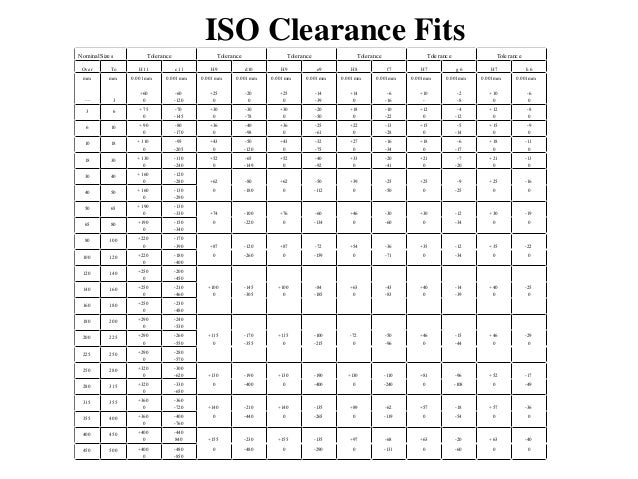
Clearance fit. Transition fit. Interference fit 1 This paragraph can be used to choose a fit and determine tolerances and deviations of machine parts according to the standard ISO 286:1988. This standard is identical with the European standard EN and defines an internationally recognized system of tolerances, deviations and fits. The standard ISO 286 is used as an international standard for linear dimension tolerances and has been accepted in most industrially developed countries in identical or modified wording as a national standard (JIS B 0401, DIN ISO 286, BS EN 20286, CSN EN 20286, etc.). The system of tolerances and fits ISO can be applied in tolerances and deviations of smooth parts and for fits created by their coupling. It is used particularly for cylindrical parts with round sections.
Tolerances and deviations in this standard can also be applied in smooth parts of other sections. Similarly, the system can be used for coupling (fits) of cylindrical parts and for fits with parts having two parallel surfaces (e.g. Fits of keys in grooves).
The term 'shaft', used in this standard has a wide meaning and serves for specification of all outer elements of the part, including those elements which do not have cylindrical shapes. Also, the term 'hole' can be used for specification of all inner elements regardless of their shape.
Note: All numerical values of tolerances and deviations mentioned in this paragraph are given in the metric system and relate to parts with dimensions specified at 20 °C. 1.1 Basic size. It is the size whose limit dimensions are specified using the upper and lower deviations. In case of a fit, the basic size of both connected elements must be the same. Attention: The standard ISO 286 defines the system of tolerances, deviations and fits only for basic sizes up to 3150 mm. 1.2 Tolerance of a basic size for specific tolerance grade. The tolerance of a size is defined as the difference between the upper and lower limit dimensions of the part.
In order to meet the requirements of various production branches for accuracy of the product, the system ISO implements 20 grades of accuracy. Each of the tolerances of this system is marked 'IT' with attached grade of accuracy (IT01, IT0, IT1.
Field of use of individual tolerances of the system ISO: IT01 to IT6 For production of gauges and measuring instruments IT5 to IT12 For fits in precision and general engineering IT11 to IT16 For production of semi-products IT16 to IT18 For structures IT11 to IT18 For specification of limit deviations of non-tolerated dimensions Note: When choosing a suitable dimension it is necessary to also take into account the used method of machining of the part in the production process. The dependency between the tolerance and modification of the surface can be found in the table in paragraph 5. 1.3 Hole tolerance zones. The tolerance zone is defined as a spherical zone limited by the upper and lower limit dimensions of the part. The tolerance zone is therefore determined by the amount of the tolerance and its position related to the basic size. The position of the tolerance zone, related to the basic size (zero line), is determined in the ISO system by a so-called basic deviation. The system ISO defines 28 classes of basic deviations for holes.
My 5-year old, Thomas, really loved seeing his favorite character Benny here and there! (It's really cute-- whenever we played the balloon game she was say 'Isa! And Marceline, my 4-year-old, really loves Isa, and she was so happy to see the cute little iguana.
These classes are marked by capital letters (A, B, C. The tolerance zone for the specified dimensions is prescribed in the drawing by a tolerance mark, which consists of a letter marking of the basic deviation and a numerical marking of the tolerance grade (e.g. H7, H8, D5, etc.).
This paragraph includes graphic illustrations of all tolerance zones of a hole which are applicable for the specified basic size 1.1 and the tolerance grade IT chosen from the pop-up list. Though the general sets of basic deviations (A.
ZC) and tolerance grades (IT1. IT18) can be used for prescriptions of hole tolerance zones by their mutual combinations, in practice only a limited range of tolerance zones is used.
An overview of tolerance zones for general use can be found in the following table. The tolerance zones not included in this table are considered special zones and their use is recommended only in technically well-grounded cases.
Example for the DIN ISO 2768-2 tolerance table. This is just one example for linear tolerances for a 100mm value. This is just one of the 8 defined ranges (30-120 mm). Engineering tolerance is the permissible limit or limits of variation in:. a physical;.
a measured value or of a material, object, system, or service;. other measured values (such as temperature, humidity, etc.);. in and, a physical or space (tolerance), as in a (lorry), or under a as well as a train in a (see and );. in the between a and a or a hole, etc.
Dimensions, properties, or conditions may have some variation without significantly affecting functioning of systems, machines, structures, etc. A variation beyond the tolerance (for example, a temperature that is too hot or too cold) is said to be noncompliant, rejected, or exceeding the tolerance. Contents. Considerations when setting tolerances A primary concern is to determine how wide the tolerances may be without affecting other factors or the outcome of a process. This can be by the use of scientific principles, engineering knowledge, and professional experience.
Experimental investigation is very useful to investigate the effects of tolerances:, formal engineering evaluations, etc. A good set of engineering tolerances in a, by itself, does not imply that compliance with those tolerances will be achieved. Actual production of any product (or operation of any system) involves some inherent variation of input and output. Measurement error and statistical uncertainty are also present in all measurements.
With a, the tails of measured values may extend well beyond plus and minus three standard deviations from the process average. Appreciable portions of one (or both) tails might extend beyond the specified tolerance. The of systems, materials, and products needs to be compatible with the specified engineering tolerances. Must be in place and an effective, such as, needs to keep actual production within the desired tolerances. A is used to indicate the relationship between tolerances and actual measured production. The choice of tolerances is also affected by the intended statistical and its characteristics such as the Acceptable Quality Level.
This relates to the question of whether tolerances must be extremely rigid (high confidence in 100% conformance) or whether some small percentage of being out-of-tolerance may sometimes be acceptable. An alternative view of tolerances and others have suggested that traditional two-sided tolerancing is analogous to 'goal posts' in a: It implies that all data within those tolerances are equally acceptable. The alternative is that the best product has a measurement which is precisely on target. There is an increasing loss which is a function of the deviation or variability from the target value of any design parameter.
The greater the deviation from target, the greater is the loss. This is described as the or 'quality loss function', and it is the key principle of an alternative system called 'inertial tolerancing'. Research and development work conducted by M.
Pillet and colleagues at the Savoy University has resulted in industry-specific adoption. Recently the publishing of the French standard NFX 04-008 has allowed further consideration by the manufacturing community. Mechanical component tolerance. Summary of basic size, fundamental deviation and IT grades compared to minimum and maximum sizes of the shaft and hole. Dimensional tolerance is related to, but different from in mechanical engineering, which is a designed-in clearance or interference between two parts. Tolerances are assigned to parts for manufacturing purposes, as boundaries for acceptable build.
No machine can hold dimensions precisely to the nominal value, so there must be acceptable degrees of variation. If a part is manufactured, but has dimensions that are out of tolerance, it is not a usable part according to the design intent. Tolerances can be applied to any dimension. The commonly used terms are:.
Basic size: the nominal diameter of the shaft (or bolt) and the hole. This is, in general, the same for both components. Lower deviation: the difference between the minimum possible component size and the basic size.
Iso 2768 Hole Tolerance
Upper deviation: the difference between the maximum possible component size and the basic size. Fundamental deviation: the minimum difference in size between a component and the basic size. This is identical to the upper deviation for shafts and the lower deviation for holes. If the fundamental deviation is greater than zero, the bolt will always be smaller than the basic size and the hole will always be wider. Fundamental deviation is a form of, rather than tolerance. International Tolerance grade: this is a standardised measure of the maximum difference in size between the component and the basic size (see below).
For example, if a shaft with a nominal diameter of 10 is to have a sliding fit within a hole, the shaft might be specified with a tolerance range from 9.964 to 10 mm (i.e. A zero fundamental deviation, but a lower deviation of 0.036 mm) and the hole might be specified with a tolerance range from 10.04 mm to 10.076 mm (0.04 mm fundamental deviation and 0.076 mm upper deviation). This would provide a clearance fit of somewhere between 0.04 mm (largest shaft paired with the smallest hole, called the 'maximum material condition') and 0.112 mm (smallest shaft paired with the largest hole).
In this case the size of the tolerance range for both the shaft and hole is chosen to be the same (0.036 mm), meaning that both components have the same International Tolerance grade but this need not be the case in general. When no other tolerances are provided, the uses the following standard tolerances: 1 decimal place (.x): ±0.2' 2 decimal places (.0x): ±0.01' 3 decimal places (.00x): ±0.005' 4 decimal places (.000x): ±0.0005'. Main article: When designing mechanical components, a system of standardized tolerances called International Tolerance grades are often used.
The standard (size) tolerances are divided into two categories: hole and shaft. They are labelled with a letter (capitals for holes and lowercase for shafts) and a number.
For example: H7 (hole, or ) and h7 (shaft or bolt). H7/h6 is a very common standard tolerance which gives a tight fit. The tolerances work in such a way that for a hole H7 means that the hole should be made slightly larger than the base dimension (in this case for an ISO fit 10+0.015−0, meaning that it may be up to 0.015 mm larger than the base dimension, and 0 mm smaller). The actual amount bigger/smaller depends on the base dimension. For a shaft of the same size h6 would mean 10+0-0.009, which means the shaft may be as small as 0.009 mm smaller than the base dimension and 0 mm larger. This method of standard tolerances is also known as Limits and Fits and can be found in.
The table below summarises the International Tolerance (IT) grades and the general applications of these grades: Measuring Tools Material IT Grade 01 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Fits Large Manufacturing Tolerances An analysis of fit by is also extremely useful: It indicates the frequency (or probability) of parts properly fitting together. Electrical component tolerance An electrical specification might call for a with a nominal value of 100 Ω , but will also state a tolerance such as '±1%'. This means that any resistor with a value in the range 99 Ω to 101 Ω is acceptable. For critical components, one might specify that the actual resistance must remain within tolerance within a specified temperature range, over a specified lifetime, and so on. Many commercially available and of standard types, and some small, are often marked with to indicate their value and the tolerance.
High-precision components of non-standard values may have numerical information printed on them. Difference between allowance and tolerance The terms are often confused but sometimes a difference is maintained. Clearance (civil engineering) In, clearance refers to the difference between the and the in the case of or, or the difference between the size of any and the width/height of doors or the height of an as well as the under a. See also. Pillet M., Adragna P-A., Germain F., Inertial Tolerancing: 'The Sorting Problem', Journal of Machine Engineering: Manufacturing Accuracy Increasing Problems, optimization, Vol. 2, 3 and 4 decimal places quoted from page 29 of 'Machine Tool Practices', 6th edition, by R.R.; Kibbe, J.E.; Neely, R.O.; Meyer & W.T.; White, 2nd printing, copyright 1999, 1995, 1991, 1987, 1982 and 1979 by Prentice Hall. (All four places, including the single decimal place, are common knowledge in the field, although a reference for the single place could not be found.).
According to Chris McCauley, Editor-In-Chief of Industrial Press': Standard Tolerance '. Does not appear to originate with any of the recent editions (24-28) of, although those tolerances may have been mentioned somewhere in one of the many old editions of the Handbook.' (4/24/2009 8:47 AM) Further reading. Pyzdek, T, 'Quality Engineering Handbook', 2003,. Godfrey, A. B., 'Juran's Quality Handbook', 1999,. ASTM D4356 Standard Practice for Establishing Consistent Test Method Tolerances External links.